First 5 things to start learning PyTorch Tensors in Sagemaker Notebooks

Let’s begin our TorchAdventure in AWS! with this 11 basic functions distributed in the following sections:

• Creating tensors: Empty() and Zeros()

• Measuring tensors: Size() and Shape(), Sum() and Dimensions

• Changing and copying tensors: Reshape(), view() and randn()

• Modifying tensors: Unsqueeze()

• Comparing tensors: Element-Wise Equality: Eq

First lets spin up a new sagemaker instance:

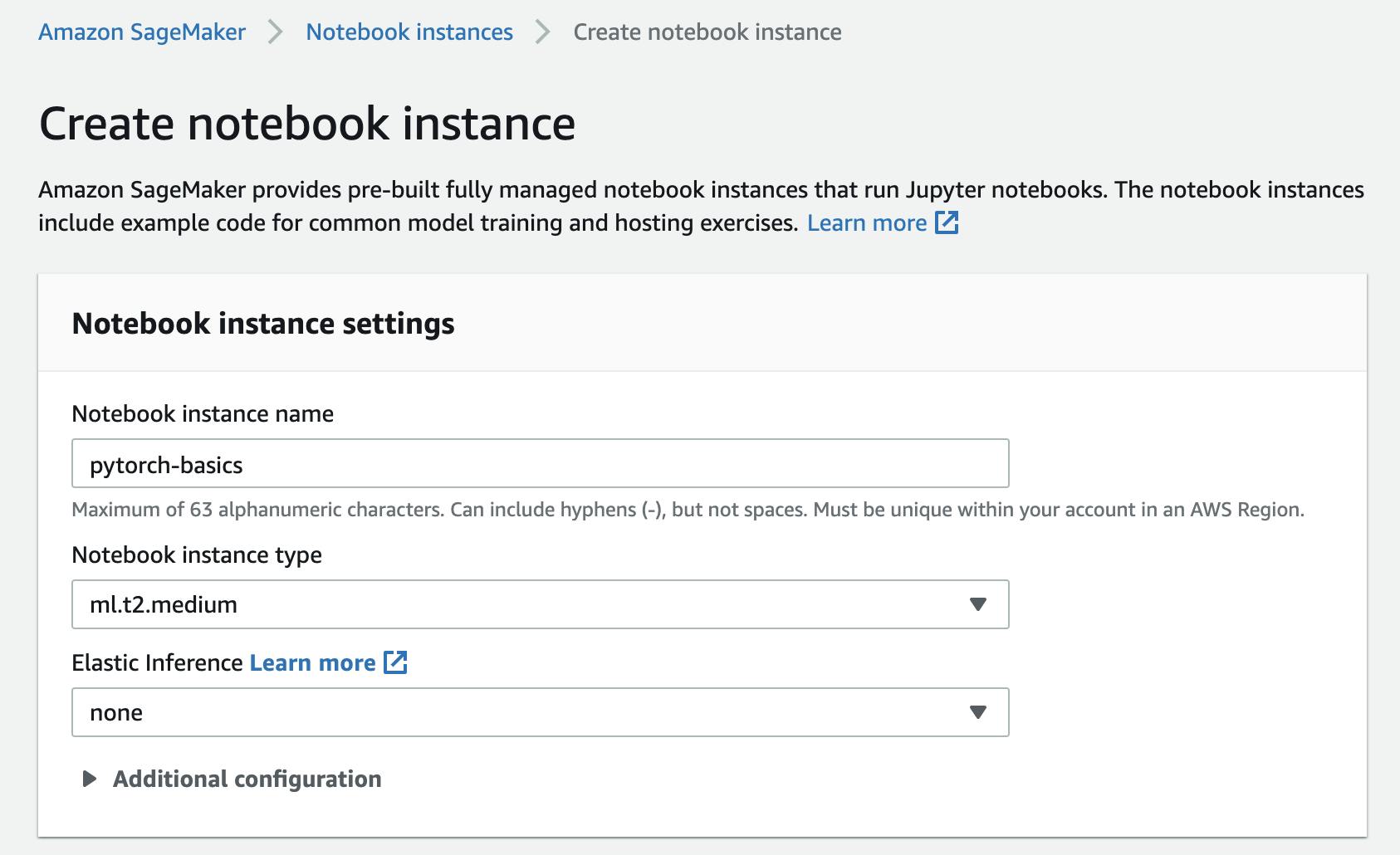
Now go to Jupyter Lab and import or create a new Notebook with this kernel for Pytorch:

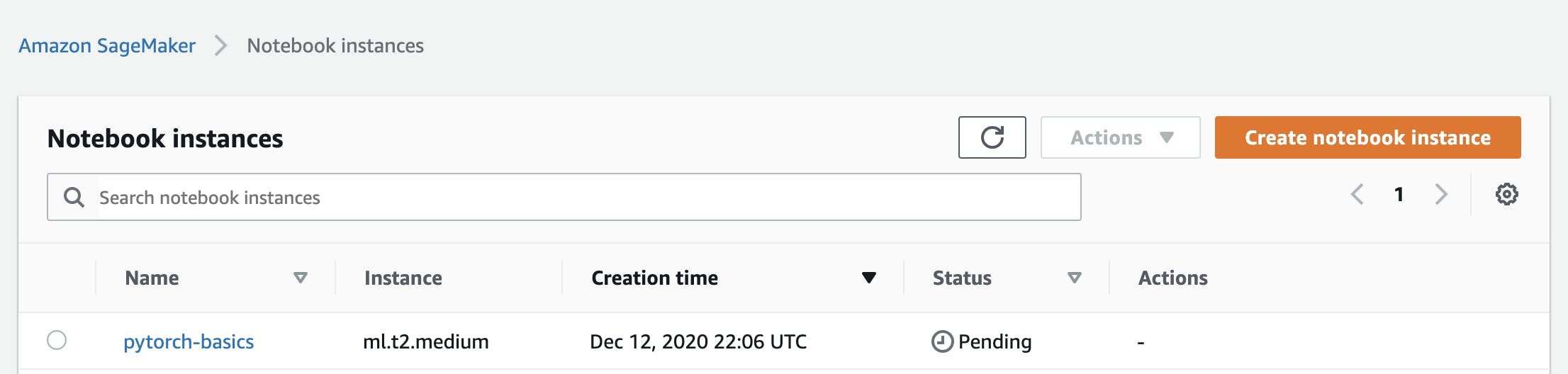
Select the appropiate kernel, for this case it could be: conda_pytorch_p36

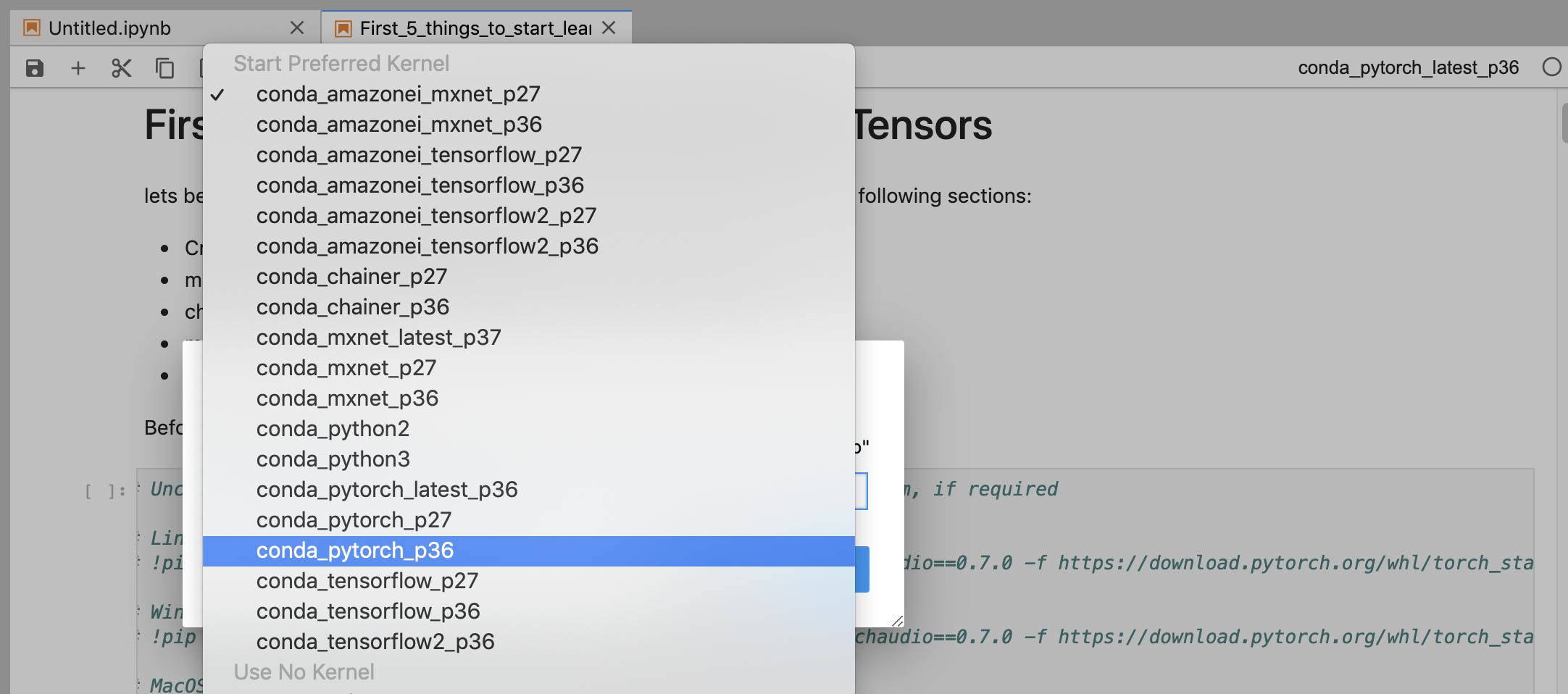
Here is where I will start from scratch.

Before we begin, let’s install and import PyTorch

*# Uncomment and run the appropriate command for your operating system, if required*

# Linux / Binder
# !pip install numpy torch==1.7.0+cpu torchvision==0.8.1+cpu torchaudio==0.7.0 -f https://download.pytorch.org/whl/torch_stable.html

# Windows
# !pip install numpy torch==1.7.0+cpu torchvision==0.8.1+cpu torchaudio==0.7.0 -f https://download.pytorch.org/whl/torch_stable.html

# MacOS
# !pip install numpy torch torchvision torchaudio

Import Pytorch from the Notebook instance

**import** **torch**

Function 1 — Empty and Zeros — how to initialize tensors

We need to start working with the basics pytorch functions, and the first thing is create our matrix

*# Creates a 3 x 2 matrix which is empty*
a = torch.empty(3, 2)
print(a)

tensor([[1.5842e-35, 0.0000e+00],
        [4.4842e-44, 0.0000e+00],
        [       nan, 0.0000e+00]])

Here is how PyTorch is allocating memory for this tensor. Whatever, it will not erase anything previous content in the memory.

by default, when you initializes a tensor is used the float32 dtype. you can review it here: https://pytorch.org/docs/stable/generated/torch.set_default_tensor_type.html#torch.set_default_tensor_type

But you can also start working with torch.zeros

*# Applying the zeros function and *
*# storing the resulting tensor*

a = torch.zeros([3, 5]) 
print("a = ", a) 

b = torch.zeros([2, 4]) 
print("b = ", b) 

c = torch.zeros([4, 1]) 
print("c = ", c) 

d = torch.zeros([4, 4, 2]) 
print("d = ", d)

the result will be:

a =  tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])
b =  tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.]])
c =  tensor([[0.],
        [0.],
        [0.],
        [0.]])
d =  tensor([[[0., 0.],
         [0., 0.],
         [0., 0.],
         [0., 0.]],

[[0., 0.],
         [0., 0.],
         [0., 0.],
         [0., 0.]],

[[0., 0.],
         [0., 0.],
         [0., 0.],
         [0., 0.]],

[[0., 0.],
         [0., 0.],
         [0., 0.],
         [0., 0.]]])

this tensor is filled with zeros, so PyTorch allocates memory and zero-initializes the tensor elements inside

You cannot change the way a tensor is created, if you create a zeros tensor, make sure is not referenced to any other.

*# correctly initialized*
a = torch.empty(3,3)
print(a)

#also correct
b = torch.empty(1,2,3)

print(b)

the results will be:

tensor([[2.4258e-35, 0.0000e+00, 1.5975e-43],
        [1.3873e-43, 1.4574e-43, 6.4460e-44],
        [1.4153e-43, 1.5274e-43, 1.5695e-43]])
tensor([[[2.3564e-35, 0.0000e+00, 1.4013e-45],
         [1.4574e-43, 6.4460e-44, 1.4153e-43]]])

Lets see now, how you cannot use the zeros function:

*# incorrect reference, you must create a new one*
c = torch.zeros(b,1) 
print("c = ", c)

output:

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-35-c044e2995879> in <module>()
**      1** # incorrect reference, you must create a new one
----> 2 c = torch.zeros(b,1)
**      3** print("c = ", c)

TypeError: zeros() received an invalid combination of arguments - got (Tensor, int), but expected one of:
 * (tuple of ints size, *, tuple of names names, torch.dtype dtype, torch.layout layout, torch.device device, bool pin_memory, bool requires_grad)
 * (tuple of ints size, *, Tensor out, torch.dtype dtype, torch.layout layout, torch.device device, bool pin_memory, bool requires_grad)

lets review the zero method closely:

Our documentation says:

Syntax: torch.zeros(size, out=None)

Parameters:
size: a sequence of integers defining the shape of the output tensor
out (Tensor, optional): the output tensor

Return type: A tensor filled with scalar value 0, of same shape as size.

torch.zeros and torch.empty are the first functions to start working with pytorch tensors and learning a little bit of matrix and vectors

Function 2 — Tensor Size, Shape and Dimension Operations

Lets understand dimensions in Pytorch.

Now lets create some tensors and determine the size of every one

**import** **torch** 
*# Create a tensor from data*
c = torch.tensor([[3.2 , 1.6, 2], [1.3, 2.5 , 6.9]])
print(c)

print(c.size())

output

tensor([[3.2000, 1.6000, 2.0000],
        [1.3000, 2.5000, 6.9000]])
torch.Size([2, 3])

Lets see torch.shape and take a closer look at how size is given here

Now in the next example lets use shape functions to get the size of a tensor

In [ ]:

x = torch.tensor([
     [1, 2, 3],
     [4, 5, 6]
   ])
x.shape
torch.Size([2, 3])

Out[ ]:

torch.Size([2, 3])

Shape and Size give us the same correct dimensions of the tensor.

in this case we have a 3D-tensor (with 3 dimensions)

Dimension 0 Dimension 1 and Dimension 2

lets create a new tensor:

In [ ]:

y = torch.tensor([
     [
       [1, 2, 3],
       [4, 5, 6]
     ],
     [
       [1, 2, 3],
       [4, 5, 6]
     ],
     [
       [1, 2, 3],
       [4, 5, 6]
     ]
   ])

y.shape

Out[ ]:

torch.Size([3, 2, 3])

Lets se how we can make operations using a 3d tensor now for every dimension layer and see how it behaves

In [ ]:

sum1 = torch.sum(y, dim=0)
print(sum1)

sum2 = torch.sum(y, dim=1)
print(sum2)

sum3 = torch.sum(y, dim=2)
print(sum3)

tensor([[ 3,  6,  9],
        [12, 15, 18]])
tensor([[5, 7, 9],
        [5, 7, 9],
        [5, 7, 9]])
tensor([[ 6, 15],
        [ 6, 15],
        [ 6, 15]])

we can see now a 3d tensor is more complicated as we advance, and we can perform custom operations within every dimension

its limited right now to 3 dims so we cannot perform this:

In []

sum2 = torch.sum(y, dim=3)
print(sum1)

Out [ ]:

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-56-7caf723c6102> in <module>()
----> 1 sum2 = torch.sum(y, dim=3)
**      2** print(sum1)

IndexError: Dimension out of range (expected to be in range of [-3, 2], but got 3)

to accomplish adding more layers of dimensions we can review the unsqueeze functions → .unsqueeze() but for now let’s go to the next basic function

Function 3 — Reshape, View and Random

There is a function in NunPy called ndarray.reshape() for reshaping an array.

Now in pytorch, there is torch.view(tensor) for the same purpose, but at the same time, there is also a torch.reshape(tensor).

let’s figure out the differences between them and when you should use either of them.

First of all we are going to use a new functions for randomize our tensor.

In [ ]:

**import** **torch** 
x = torch.randn(5, 3)

print(x)

Out []

tensor([[-0.5793,  0.6999,  1.7417],
        [-0.9810,  0.0626,  0.4100],
        [-0.6519, -0.0595, -1.2156],
        [-0.3973, -0.3103,  1.6253],
        [ 0.2775, -0.0045, -0.2985]])

this is basic usage of torch.randm, so now lets use View from another variable “y” and describe all elements

In [ ]:

*# Return a view of the x, but only having *
*# one dimension and max number of elements*
y = x.view(5 * 3)

*#lets see the size of every tensor*
print("lets see the size of every tensor")
print('Size of x:', x.size())
print('Size of y:', y.size())

*#and the elements of very tensor to compare*
print("and the elements of very tensor to compare")
print("X:", x)
print("Y:", y)

Out []

lets see the size of every tensor
Size of x: torch.Size([5, 3])
Size of y: torch.Size([15])
and the elements of very tensor to compare
X: tensor([[-0.5793,  0.6999,  1.7417],
        [-0.9810,  0.0626,  0.4100],
        [-0.6519, -0.0595, -1.2156],
        [-0.3973, -0.3103,  1.6253],
        [ 0.2775, -0.0045, -0.2985]])
Y: tensor([-0.5793,  0.6999,  1.7417, -0.9810,  0.0626,  0.4100, -0.6519, -0.0595,
        -1.2156, -0.3973, -0.3103,  1.6253,  0.2775, -0.0045, -0.2985])

take a look at Y tensor, it only has 1 dimension. so Viewing another tensor may be difficult for some operations

Now lets use Reshape to replicate the exact dimensions of X

In [ ]:

*# Get back the original tensor with reshape()*
z = y.reshape(5, 3)
print(z)

tensor([[-0.2927,  0.0329,  0.8485],
        [ 1.9581,  0.8313, -0.1529],
        [-0.2330, -0.1887,  1.8206],
        [ 1.5252,  1.0909,  0.0547],
        [-0.1231, -0.4238, -0.6724]])

we cannot only reshape the original, we can also change the dimensions with some limited actions related to the maximum elements:

first lets reshape to 1 more dimension

In [ ]:

*# Get back the original tensor with reshape()*
z = y.reshape(15)
print(z)

#reshaping 15 elements, 1 dim
z = y.reshape(3*5)
print(z)

#reshaping in different order, 3 dimensions
z = y.reshape(3,5)
print(z)

#Reshaping with more dimensions but its 15 elements always
z = y.reshape(3,5,1)
print(z)

tensor([-0.5793,  0.6999,  1.7417, -0.9810,  0.0626,  0.4100, -0.6519, -0.0595,
        -1.2156, -0.3973, -0.3103,  1.6253,  0.2775, -0.0045, -0.2985])
tensor([-0.5793,  0.6999,  1.7417, -0.9810,  0.0626,  0.4100, -0.6519, -0.0595,
        -1.2156, -0.3973, -0.3103,  1.6253,  0.2775, -0.0045, -0.2985])
tensor([[-0.5793,  0.6999,  1.7417, -0.9810,  0.0626],
        [ 0.4100, -0.6519, -0.0595, -1.2156, -0.3973],
        [-0.3103,  1.6253,  0.2775, -0.0045, -0.2985]])
tensor([[[-0.5793],
         [ 0.6999],
         [ 1.7417],
         [-0.9810],
         [ 0.0626]],

        [[ 0.4100],
         [-0.6519],
         [-0.0595],
         [-1.2156],
         [-0.3973]],

        [[-0.3103],
         [ 1.6253],
         [ 0.2775],
         [-0.0045],
         [-0.2985]]])

Now lets reshape exceeding the number of elements in the tensor:

In [ ]:

z = y.reshape(16)
print(z)

Out []

---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-78-c7ae174fce73> in <module>()
----> 1 z = y.reshape(16)
**      2** print(z)

RuntimeError: shape '[16]' is invalid for input of size 15

it will fail also for z = y.reshape(3*6) or putting more elements that does not exist in the tensor.

Now let’s keep going to the next section.

Function 4 — Unsqueeze()

Mainly, it allows us to add more dimensions at specific index you define.

lets take a look:

In [ ]:

**import** **torch**

#dim=1, that is (3)
x = torch.tensor([1, 2, 3])
print('x: ', x)
print('x.size: ', x.size())

#x1 becomes a matrix of (3,1)
x1 = torch.unsqueeze(x, 1)
print('x1: ', x1)
print('x1.size: ', x1.size())

Out []

x:  tensor([1, 2, 3])
x.size:  torch.Size([3])
x1:  tensor([[1],
        [2],
        [3]])
x1.size:  torch.Size([3, 1])
x2:  tensor([[1, 2, 3]])
x2.size:  torch.Size([1, 3])

Our initial tensor is Tensor([1,2,3]), and the output size is [3].

And then we proceed with adding 1 dimenson with unsqueeze operation, namely torch.unsqueeze(x, 1), the size of x1 is [3,1].

In [ ]:

*#x2 becomes a matrix of (1,3)*
x2 = torch.unsqueeze(x, 0)
print('x2: ', x2)
print('x2.size: ', x2.size())

Out []

x2:  tensor([[1, 2, 3]])
x2.size:  torch.Size([1, 3])

When we perform torch.unsqueeze(x, 0), the size of x2 is [1,3].

In [ ]:

*# Example 3 - breaking (to illustrate when it breaks)*


print(x.unsqueeze())

Out []

---------------------------------------------------------------------------
TypeError  Traceback (most recent call last)
<ipython-input-89-5a320a828907> in <module>()
**      2** 
**      3** 
----> 4 print(x.unsqueeze())

TypeError: unsqueeze() missing 1 required positional arguments: "dim"

We must specified the dimension correctly, although we are just adding 1 dim, it is necessary to put like this: x.unqueeze(0)

Function 5 — Torch Eq (Element Wise equality)

This function is under comparison category and it computes equality in element-wise and returns a boolean tensor. True if equal, False otherwise.

Lets review how we can operate with different sizes of tensors:

In [ ]:

*# Example 1 - working *
x1 = torch.tensor([[1, 2], [3, 4.]])
x2 = torch.tensor([[2, 2], [2, 5]])
x3 = torch.randn(3,5)

#size x1 and z2
print(x1.size())
print(x2.size())

# tensors 1 and 2
print(x1)
print(x2)


#size x3
print(x3.size())

#tensors 3
print(x3)

torch.eq(x1,x2)

torch.Size([2, 2])
torch.Size([2, 2])
tensor([[1., 2.],
        [3., 4.]])
tensor([[2, 2],
        [2, 5]])
torch.Size([3, 5])
tensor([[-1.3040, -0.4658, -0.5269,  0.7409,  0.9135],
        [ 1.0780,  2.0584, -0.9629, -1.1412, -0.3105],
        [ 0.3613, -1.4196,  2.1145,  0.3649,  0.2037]])

Out[ ]:

tensor([[False,  True],
        [False, False]])

x1 and x3 have the same size, but x3 is [3,5], has bigger size.

comparing x1 and x2 is Ok.

In [ ]:

*# Example 2 - working (with broadcasting)*
x4 = torch.tensor([[1, 2], [3, 4]])
print(x4.size())
x5 = torch.tensor([2, 5])
print(x5.size())
torch.eq(x4, x5)

torch.Size([2, 2])
torch.Size([2])

Out[ ]:

tensor([[False, False],
        [False, False]])

we can also compare, different sizes only if the seconf value, in this case x5, that has size of [2] is broadcastable with the frist one thst is [2,2]

In [ ]:

*# Example 3 - breaking (to illustrate when it breaks)*
x6 = torch.tensor([[0, 2, 4], [3, 4, 5]])
print(x6.size())
x7 = torch.tensor([[2, 3], [2, 4]])
print(x7.size())

torch.eq(x6, x3)

torch.Size([2, 3])
torch.Size([2, 2])

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
<ipython-input-98-ac2ad1ecd5b0> in <module>()
      5 print(x7.size())
      6 
----> 7 torch.eq(x6, x3)

RuntimeError: The size of tensor a (3) must match the size of tensor b (5) at non-singleton dimension 1

finally, we cant compare different sizes if the second arguments shape is not broadcastable with the first argument.

Conclusion

we review 5 basic topics covering more than 10 PyTorch functions.

in the next post i’ll talk about Linear Regression.

Reference Links

Provide links to your references and other interesting articles about tensors

• Official documentation for tensor operations: https://pytorch.org/docs/stable/torch.html

• Squeeze and unsqueeze functions here: https://www.programmersought.com/article/65705814717/

• Understanding dimensions in Pytorch: https://towardsdatascience.com/understanding-dimensions-in-pytorch-6edf9972d3be

#aws #reinvent2020 #awsperu #awsugperu #awscloud

Carlos Cortez — AWS UG Perú Leader / AWS ML Community Builder ccortez@aws.pe @ccortezb Podcast: imperiocloud.com @imperiocloud twitch.tv/awsugperu cennticloud.thinkific.com Carlos Cortez ML Engineer — Senior Cloud Architect — Pro Services Cluster — BGH Tech Partner |… Hello Everyone, I’m the Founder of AWS User Group Perú 🇵🇪 (2014) and also an AWS Solutions Architect Certified…linkedin.com